Trigonometría - Seno, Coseno y Tangente
Trigonometría: Seno, Coseno y Tangente en triángulos rectángulos
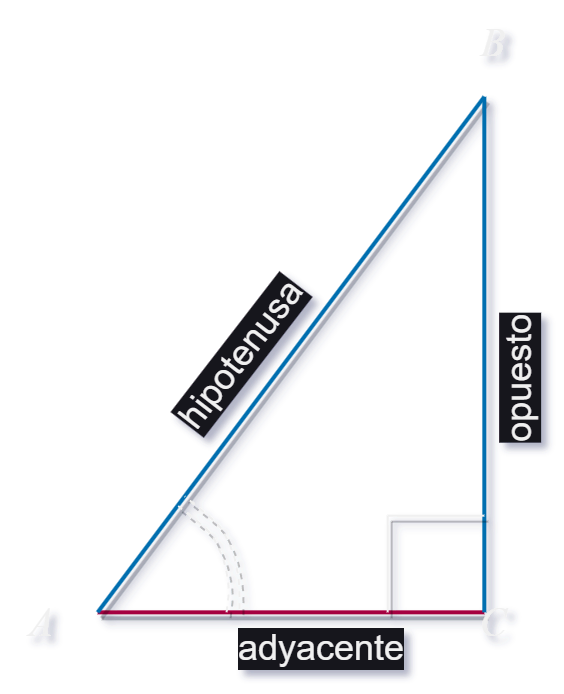
Triángulos rectángulos
En un triángulo rectángulo hay un ángulo de 90 grados, al que llamamos ángulo recto. El lado opuesto a este ángulo se llama cateto opuesto (co), el lado adyacente se llama cateto adyacente (ca) y el lado más largo opuesto al ángulo recto se llama hipotenusa (H).
Seno (sin)
El seno de un ángulo en un triángulo rectángulo es la relación entre la longitud del cateto opuesto (co) y la longitud de la hipotenusa (H).
Para calcular el seno de un ángulo, simplemente dividimos la longitud del cateto opuesto (co) entre la longitud de la hipotenusa (H). El seno nos indica qué tan grande es el ángulo en relación con la hipotenusa (H). Un valor de seno grande indica un ángulo pronunciado, mientras que un valor pequeño de seno indica un ángulo plano.
Coseno (cos)
El coseno de un ángulo en un triángulo rectángulo es la relación entre la longitud del cateto adyacente (ca) y la longitud de la hipotenusa (H).
Para calcular el coseno de un ángulo, dividimos la longitud del cateto adyacente (ca) entre la longitud de la hipotenusa (H). El coseno nos indica qué tan grande es el ángulo en relación con la hipotenusa (H), pero desde una perspectiva diferente al seno. Si el seno es grande, el coseno será pequeño y viceversa. Esto significa que si un ángulo es pronunciado, el otro ángulo será plano y viceversa.
Tangente (tan)
La tangente de un ángulo en un triángulo rectángulo es la relación entre la longitud del cateto opuesto (co) y la longitud del cateto adyacente (ca).
La tangente nos muestra qué tan grande es el ángulo en relación con el cateto adyacente (ca). Un valor de tangente grande indica un ángulo pronunciado en relación con el cateto adyacente (ca), mientras que un valor pequeño de tangente indica un ángulo plano en relación con el cateto adyacente (ca).
Estas simples relaciones (Seno, Coseno y Tangente) nos ayudan a comprender la relación entre las longitudes de los lados y los ángulos en un triángulo rectángulo y tienen muchas aplicaciones prácticas en matemáticas, ciencias y tecnología.
¡Pruébalo tú mismo y descubre el fascinante mundo de la Trigonometría!
Triángulos no rectángulos
Para triángulos no rectángulos, podemos utilizar la Ley de Cosenos y la Ley de Senos para calcular longitudes de lados y ángulos.
Ley de Cosenos
La Ley de Cosenos establece que el cuadrado de un lado de un triángulo es igual a la suma de los cuadrados de los otros dos lados menos el doble del producto de esos lados y el coseno del ángulo opuesto.
La Ley de Cosenos nos permite calcular las longitudes de los lados de un triángulo no rectángulo si conocemos el tamaño de los ángulos y las longitudes de los otros lados.
Ley de Senos
La Ley de Senos establece que la razón de la longitud de un lado al seno del ángulo opuesto en un triángulo es constante.
Con la ayuda de la Ley de Senos, podemos calcular las longitudes de los lados o el tamaño de los ángulos en un triángulo no rectángulo si conocemos la longitud de un lado y el ángulo opuesto.
Ejemplo: Cálculos de un triángulo
Tenemos un triángulo con los valores dados:
Ángulo A = 110°25’36” Lado b = 92 m Lado c = 24 m
Nuestra tarea es calcular los valores faltantes: Ángulo B, Ángulo C y Lado a.
Paso 1: Cálculo del Lado a
Podemos calcular las longitudes de los lados utilizando la Ley de los cosenos:
De aquí obtenemos:
Paso 2: Cálculo del Ángulo B
Comenzamos con la ecuación:
Para aislar el Ángulo B, podemos multiplicar ambos lados por b:
Para aislar el Ángulo B, aplicamos la función inversa del seno (Arcseno o sin⁻¹) en ambos lados:
Dado que la función inversa del seno se cancela a sí misma, obtenemos:
Ahora, con la derivación de la fórmula, podemos usarla para calcular el Ángulo B:
Paso 3: Cálculo del Ángulo C
Dado que la suma de los ángulos internos de un triángulo es 180°, podemos calcular el Ángulo C:
La Trigonometría nos abre un mundo fascinante de cálculos y relaciones geométricas que se aplican en muchas áreas.
¡Pruébalo tú mismo y descubre el fascinante mundo de la Trigonometría!