Trigonometry: Sine, Cosine, and Tangent in Right-Angled Triangles

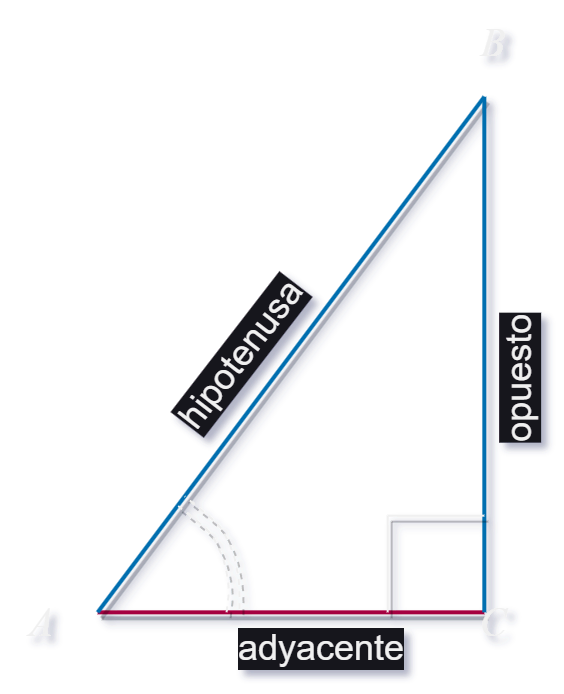
Right-Angled Triangles

In a right-angled triangle, there is an angle of 90 degrees, which we call the right angle. The side opposite this angle is called the opposite side (co), the side adjacent to it is called the adjacent side (ca), and the longest side opposite the right angle is called the hypotenuse (H).

Desktop View

Sine (sin)

The sine of an angle in a right-angled triangle is the ratio of the length of the opposite side (co) to the length of the hypotenuse (H).

To calculate the sine of an angle, we simply divide the length of the opposite side (co) by the length of the hypotenuse (H). The sine tells us how large the angle is in relation to the hypotenuse (H). A large sine value indicates a steep angle, while a small sine value indicates a shallow angle.

Cosine (cos)

The cosine of an angle in a right-angled triangle is the ratio of the length of the adjacent side (ca) to the length of the hypotenuse (H).

To calculate the cosine of an angle, we divide the length of the adjacent side (ca) by the length of the hypotenuse (H). The cosine tells us how large the angle is in relation to the hypotenuse (H), but from a different perspective than the sine. If the sine is large, the cosine is small, and vice versa. This means that if one angle is steep, the other angle is shallow.

Tangent (tan)

The tangent of an angle in a right-angled triangle is the ratio of the length of the opposite side (co) to the length of the adjacent side (ca).

The tangent shows us how large the angle is in relation to the adjacent side (ca). A large tangent value indicates a steep angle in relation to the adjacent side (ca), while a small tangent value indicates a shallow angle in relation to the adjacent side (ca).

These simple ratios (Sine, Cosine, and Tangent) help us understand the relationship between the side lengths and angles in a right-angled triangle and find many practical applications in mathematics, science, and technology.

Try it out yourself and explore the fascinating world of Trigonometry!

Non-Right-Angled Triangles

For non-right-angled triangles, we can use the Law of Cosines and the Law of Sines to calculate side lengths and angles.

Law of Cosines

The Law of Cosines states that the square of one side of a triangle is equal to the sum of the squares of the other two sides minus twice the product of these sides and the cosine of the opposite angle.

The Law of Cosines allows us to calculate the lengths of the sides of a non-right-angled triangle when we know the sizes of the angles and the lengths of the other sides.

Law of Sines

The Law of Sines states that the ratio of the length of one side to the sine of the opposite angle in a triangle is constant.

Using the Law of Sines, we can calculate the lengths of the sides or the sizes of the angles in a non-right-angled triangle when we know the length of one side and the opposite angle.

Example: Triangle Calculations

We are dealing with a triangle with the following given values:

Angle A = 110°25’36” Side b = 92 m Side c = 24 m

Our objective is to calculate the missing values: Angle B, Angle C, and Side a.

Step 1: Calculation of Side a

We can calculate the lengths of the sides using the Law of Cosines:

As a result:

Step 2: Calculation of Angle B

We start with the equation:

To isolate Angle B, we can multiply both sides by b:
To isolate Angle B, we apply the inverse sine function (Arcsine or sin⁻¹) to both sides:
Since the inverse sine function cancels itself out, we get: