Trigonometrie: Sinus, Kosinus und Tangens in rechtwinkligen Dreiecken

Rechtwinklige Dreiecke

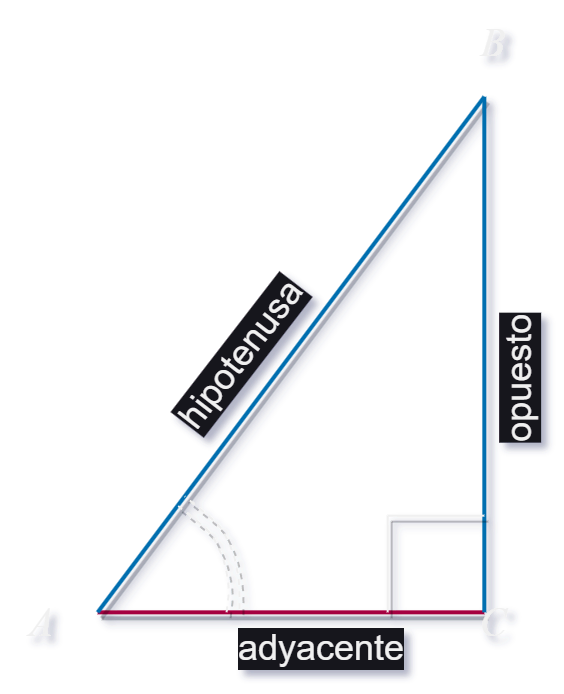
In einem rechtwinkligen Dreieck gibt es einen Winkel von 90 Grad, den wir als rechten Winkel bezeichnen. Die gegenüberliegende Seite dieses Winkels wird als Gegenkathete (co) bezeichnet, die angrenzende Seite als Ankathete (ca) und die längste Seite gegenüber dem rechten Winkel wird als Hypotenuse (H) bezeichnet.

Desktop View

Sinus (sin)

Der Sinus eines Winkels in einem rechtwinkligen Dreieck ist das Verhältnis der Länge der Gegenkathete (co) zur Länge der Hypotenuse (H).

Um den Sinus eines Winkels zu berechnen, teilen wir also einfach die Länge der Gegenkathete (co) durch die Länge der Hypotenuse (H). Der Sinus gibt uns an, wie groß der Winkel im Verhältnis zur Hypotenuse (H) ist. Ein großer Sinus-Wert bedeutet einen steilen Winkel, während ein kleiner Sinus-Wert auf einen flachen Winkel hinweist.

Kosinus (cos)

Der Kosinus eines Winkels in einem rechtwinkligen Dreieck ist das Verhältnis der Länge der Ankathete (ca) zur Länge der Hypotenuse (H).

Um den Kosinus eines Winkels zu berechnen, teilen wir die Länge der Ankathete (ca) durch die Länge der Hypotenuse (H). Der Kosinus gibt uns an, wie groß der Winkel im Verhältnis zur Hypotenuse (H) ist, aber aus einer anderen Perspektive als der Sinus. Wenn der Sinus groß ist, ist der Kosinus klein und umgekehrt. Das bedeutet, wenn ein Winkel steil ist, ist der andere Winkel flach und umgekehrt.

Tangens (tan)

Der Tangens eines Winkels in einem rechtwinkligen Dreieck ist das Verhältnis der Länge der Gegenkathete (co) zur Länge der Ankathete (ca).

Der Tangens zeigt uns, wie groß der Winkel im Verhältnis zur Ankathete (ca) ist. Ein großer Tangens-Wert bedeutet einen steilen Winkel im Verhältnis zur Ankathete (ca), während ein kleiner Tangens-Wert auf einen flachen Winkel im Verhältnis zur Ankathete (ca) hinweist.

Diese einfachen Verhältnisse (Sinus, Kosinus und Tangens) helfen uns, die Beziehung zwischen den Seitenlängen und Winkeln in einem rechtwinkligen Dreieck zu verstehen und viele praktische Anwendungen in der Mathematik, Wissenschaft und Technik zu finden.

Probier es selbst aus und entdecke die faszinierende Welt der Trigonometrie!

Nicht rechtwinklige Dreiecke

Für nicht rechtwinklige Dreiecke können wir den Satz von Cosinus und den Satz von Sinus verwenden, um Seitenlängen und Winkel zu berechnen.

Satz von Cosinus

Der Satz von Cosinus besagt, dass das Quadrat einer Seite eines Dreiecks gleich der Summe der Quadrate der anderen beiden Seiten abzüglich des doppelten Produkts dieser Seiten und des Kosinus des entgegengesetzten Winkels ist.

Der Satz von Cosinus ermöglicht es uns, die Längen der Seiten eines nicht rechtwinkligen Dreiecks zu berechnen, wenn wir die Größe der Winkel und die Längen der anderen Seiten kennen.

Satz von Sinus

Der Satz von Sinus besagt, dass das Verhältnis der Länge einer Seite zu dem Sinus des entgegengesetzten Winkels in einem Dreieck konstant ist.

Mit Hilfe des Satzes von Sinus können wir die Längen der Seiten oder die Größe der Winkel in einem nicht rechtwinkligen Dreieck berechnen, wenn wir die Länge einer Seite und den entgegengesetzten Winkel kennen.

Beispiel: Dreiecksberechnungen

Wir haben ein Dreieck mit den gegebenen Werten:

Winkel A = 110°25’36”
Seite b = 92 m
Seite c = 24 m

Unsere Aufgabe ist es, die fehlenden Werte zu berechnen: Winkel B, Winkel C und Seite a.

Schritt 1: Berechnung von Seite a

Wir können die Seitenlängen mithilfe des Cosinussatzes berechnen:

Daraus ergibt sich:

Schritt 2: Berechnung von Winkel B

Wir starten mit der Gleichung:

Um Winkel B zu isolieren, können wir die Multiplikation beider Seiten mit b durchführen:
Um Winkel B zu isolieren, wenden wir die Umkehrfunktion des Sinus an (Arcsin oder sin⁻¹) auf beide Seiten:
Da die Umkehrfunktion des Sinus auf sich selbst “kürzt”, erhalten wir: